QMatrix

The QMatrix class specifies 2D transformations of a coordinate system. More…

Inheritance diagram of PySide2.QtGui.QMatrix

Synopsis

Functions

Detailed Description

A matrix specifies how to translate, scale, shear or rotate the coordinate system, and is typically used when rendering graphics. QMatrix , in contrast to QTransform , does not allow perspective transformations. QTransform is the recommended transformation class in Qt.

A QMatrix object can be built using the setMatrix() , scale() , rotate() , translate() and shear() functions. Alternatively, it can be built by applying basic matrix operations . The matrix can also be defined when constructed, and it can be reset to the identity matrix (the default) using the reset() function.

The QMatrix class supports mapping of graphic primitives: A given point, line, polygon, region, or painter path can be mapped to the coordinate system defined by this matrix using the map() function. In case of a rectangle, its coordinates can be transformed using the mapRect() function. A rectangle can also be transformed into a polygon (mapped to the coordinate system defined by this matrix), using the mapToPolygon() function.

QMatrix provides the isIdentity() function which returns true if the matrix is the identity matrix, and the isInvertible() function which returns true if the matrix is non-singular (i.e. AB = BA = I). The inverted() function returns an inverted copy of this matrix if it is invertible (otherwise it returns the identity matrix). In addition, QMatrix provides the determinant() function returning the matrix’s determinant.

Finally, the QMatrix class supports matrix multiplication, and objects of the class can be streamed as well as compared.

Rendering Graphics

When rendering graphics, the matrix defines the transformations but the actual transformation is performed by the drawing routines in QPainter .

By default, QPainter operates on the associated device’s own coordinate system. The standard coordinate system of a QPaintDevice has its origin located at the top-left position. The x values increase to the right; y values increase downward. For a complete description, see the coordinate system documentation.

QPainter has functions to translate, scale, shear and rotate the coordinate system without using a QMatrix . For example:

qmatrix-simpletransformation1

 
def paintEvent(self, event):
    painter = QPainter(self)
    painter.setPen(QPen(Qt.blue, 1, Qt.DashLine))
    painter.drawRect(0, 0, 100, 100)

    painter.rotate(45)

    painter.setFont(QFont("Helvetica", 24))
    painter.setPen(QPen(Qt.black, 1))
    painter.drawText(20, 10, "QMatrix")

Although these functions are very convenient, it can be more efficient to build a QMatrix and call setMatrix() if you want to perform more than a single transform operation. For example:

qmatrix-combinedtransformation2

 
def paintEvent(self, event)

    painter = QPainter(self)
    painter.setPen(QPen(Qt.blue, 1, Qt.DashLine))
    painter.drawRect(0, 0, 100, 100)

    matrix = QMatrix()
    matrix.translate(50, 50)
    matrix.rotate(45)
    matrix.scale(0.5, 1.0)
    painter.setMatrix(matrix)

    painter.setFont(QFont("Helvetica", 24))
    painter.setPen(QPen(Qt.black, 1))
    painter.drawText(20, 10, "QMatrix")

Basic Matrix Operations

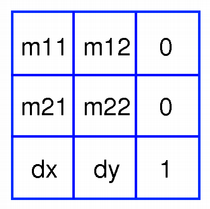
../../_images/qmatrix-representation.png

A QMatrix object contains a 3 x 3 matrix. The dx and dy elements specify horizontal and vertical translation. The m11 and m22 elements specify horizontal and vertical scaling. And finally, the m21 and m12 elements specify horizontal and vertical shearing .

QMatrix transforms a point in the plane to another point using the following formulas:

x' = m11*x + m21*y + dx
y' = m22*y + m12*x + dy

The point (x, y) is the original point, and (x’, y’) is the transformed point. (x’, y’) can be transformed back to (x, y) by performing the same operation on the inverted() matrix.

The various matrix elements can be set when constructing the matrix, or by using the setMatrix() function later on. They can also be manipulated using the translate() , rotate() , scale() and shear() convenience functions, The currently set values can be retrieved using the m11() , m12() , m21() , m22() , dx() and dy() functions.

Translation is the simplest transformation. Setting dx and dy will move the coordinate system dx units along the X axis and dy units along the Y axis. Scaling can be done by setting m11 and m22 . For example, setting m11 to 2 and m22 to 1.5 will double the height and increase the width by 50%. The identity matrix has m11 and m22 set to 1 (all others are set to 0) mapping a point to itself. Shearing is controlled by m12 and m21 . Setting these elements to values different from zero will twist the coordinate system. Rotation is achieved by carefully setting both the shearing factors and the scaling factors.

Here’s the combined transformations example using basic matrix operations:

qmatrix-combinedtransformation3

 
def paintEvent(self, event)

    pi = 3.14

    a    = pi/180 * 45.0
    sina = sin(a)
    cosa = cos(a)

    translationMatrix = QMatrix(1, 0, 0, 1, 50.0, 50.0)
    rotationMatrix = QMatrix(cosa, sina, -sina, cosa, 0, 0)
    scalingMatrix = QMatrix(0.5, 0, 0, 1.0, 0, 0)

    matrix = QMatrix()
    matrix =  scalingMatrix * rotationMatrix * translationMatrix

    painter = QPainter(self)
    painter.setPen(QPen(Qt.blue, 1, Qt::DashLine))
    painter.drawRect(0, 0, 100, 100)

    painter.setMatrix(matrix)

    painter.setFont(QFont("Helvetica", 24))
    painter.setPen(QPen(Qt.black, 1))
    painter.drawText(20, 10, "QMatrix")

See also

QPainter QTransform Coordinate System Affine Transformations Example Transformations Example

class PySide2.QtGui.QMatrix

PySide2.QtGui.QMatrix(other)

PySide2.QtGui.QMatrix(m11, m12, m21, m22, dx, dy)

param m12:

float

param dx:

float

param dy:

float

param other:

PySide2.QtGui.QMatrix

param m21:

float

param m22:

float

param m11:

float

Constructs an identity matrix.

All elements are set to zero except m11 and m22 (specifying the scale), which are set to 1.

See also

reset()

Constructs a matrix with the elements, m11 , m12 , m21 , m22 , dx and dy .

See also

setMatrix()

PySide2.QtGui.QMatrix.__reduce__()
Return type:

object

PySide2.QtGui.QMatrix.__repr__()
Return type:

object

PySide2.QtGui.QMatrix.determinant()
Return type:

float

Returns the matrix’s determinant.

PySide2.QtGui.QMatrix.dx()
Return type:

float

Returns the horizontal translation factor.

See also

translate() Basic Matrix Operations

PySide2.QtGui.QMatrix.dy()
Return type:

float

Returns the vertical translation factor.

See also

translate() Basic Matrix Operations

PySide2.QtGui.QMatrix.inverted()
Return type:

PyTuple

Returns an inverted copy of this matrix.

If the matrix is singular (not invertible), the returned matrix is the identity matrix. If invertible is valid (i.e. not 0), its value is set to true if the matrix is invertible, otherwise it is set to false.

See also

isInvertible()

PySide2.QtGui.QMatrix.isIdentity()
Return type:

bool

Returns true if the matrix is the identity matrix, otherwise returns false .

See also

reset()

PySide2.QtGui.QMatrix.isInvertible()
Return type:

bool

Returns true if the matrix is invertible, otherwise returns false .

See also

inverted()

PySide2.QtGui.QMatrix.m11()
Return type:

float

Returns the horizontal scaling factor.

See also

scale() Basic Matrix Operations

PySide2.QtGui.QMatrix.m12()
Return type:

float

Returns the vertical shearing factor.

See also

shear() Basic Matrix Operations

PySide2.QtGui.QMatrix.m21()
Return type:

float

Returns the horizontal shearing factor.

See also

shear() Basic Matrix Operations

PySide2.QtGui.QMatrix.m22()
Return type:

float

Returns the vertical scaling factor.

See also

scale() Basic Matrix Operations

PySide2.QtGui.QMatrix.map(x, y)
Parameters:

  • x – float

  • y – float

Maps the given coordinates x and y into the coordinate system defined by this matrix. The resulting values are put in *``tx`` and *``ty`` , respectively.

The coordinates are transformed using the following formulas:

x' = m11*x + m21*y + dx
y' = m22*y + m12*x + dy

The point (x, y) is the original point, and (x’, y’) is the transformed point.

See also

Basic Matrix Operations

PySide2.QtGui.QMatrix.map(x, y)
Parameters:

  • x – int

  • y – int

This is an overloaded function.

Maps the given coordinates x and y into the coordinate system defined by this matrix. The resulting values are put in *``tx`` and *``ty`` , respectively. Note that the transformed coordinates are rounded to the nearest integer.

PySide2.QtGui.QMatrix.map(r)
Parameters:

r – PySide2.QtGui.QRegion

Return type:

PySide2.QtGui.QRegion

PySide2.QtGui.QMatrix.map(a)
Parameters:

a – PySide2.QtGui.QPolygonF

Return type:

PySide2.QtGui.QPolygonF

PySide2.QtGui.QMatrix.map(a)
Parameters:

a – PySide2.QtGui.QPolygon

Return type:

PySide2.QtGui.QPolygon

PySide2.QtGui.QMatrix.map(p)
Parameters:

p – PySide2.QtCore.QPoint

Return type:

QPoint

PySide2.QtGui.QMatrix.map(p)
Parameters:

p – PySide2.QtGui.QPainterPath

Return type:

PySide2.QtGui.QPainterPath

PySide2.QtGui.QMatrix.map(l)
Parameters:

l – PySide2.QtCore.QLineF

Return type:

PySide2.QtCore.QLineF

PySide2.QtGui.QMatrix.map(l)
Parameters:

l – PySide2.QtCore.QLine

Return type:

PySide2.QtCore.QLine

PySide2.QtGui.QMatrix.map(p)
Parameters:

p – PySide2.QtCore.QPointF

Return type:

PySide2.QtCore.QPointF

PySide2.QtGui.QMatrix.mapRect(arg__1)
Parameters:

arg__1 – PySide2.QtCore.QRect

Return type:

PySide2.QtCore.QRect

PySide2.QtGui.QMatrix.mapRect(arg__1)
Parameters:

arg__1 – PySide2.QtCore.QRectF

Return type:

PySide2.QtCore.QRectF

PySide2.QtGui.QMatrix.mapToPolygon(r)
Parameters:

r – PySide2.QtCore.QRect

Return type:

PySide2.QtGui.QPolygon

Creates and returns a QPolygon representation of the given rectangle , mapped into the coordinate system defined by this matrix.

The rectangle’s coordinates are transformed using the following formulas:

x' = m11*x + m21*y + dx
y' = m22*y + m12*x + dy

Polygons and rectangles behave slightly differently when transformed (due to integer rounding), so matrix.map(QPolygon(rectangle)) is not always the same as matrix.mapToPolygon(rectangle) .

See also

mapRect() Basic Matrix Operations

PySide2.QtGui.QMatrix.__ne__(arg__1)
Parameters:

arg__1 – PySide2.QtGui.QMatrix

Return type:

bool

Returns true if this matrix is not equal to the given matrix , otherwise returns false .

PySide2.QtGui.QMatrix.__mul__(o)
Parameters:

o – PySide2.QtGui.QMatrix

Return type:

PySide2.QtGui.QMatrix

Returns the result of multiplying this matrix by the given matrix .

Note that matrix multiplication is not commutative, i.e. a*b != b*a.

PySide2.QtGui.QMatrix.__imul__(arg__1)
Parameters:

arg__1 – PySide2.QtGui.QMatrix

Return type:

PySide2.QtGui.QMatrix

This is an overloaded function.

Returns the result of multiplying this matrix by the given matrix .

PySide2.QtGui.QMatrix.__eq__(arg__1)
Parameters:

arg__1 – PySide2.QtGui.QMatrix

Return type:

bool

Returns true if this matrix is equal to the given matrix , otherwise returns false .

PySide2.QtGui.QMatrix.reset()

Resets the matrix to an identity matrix, i.e. all elements are set to zero, except m11 and m22 (specifying the scale) which are set to 1.

See also

QMatrix() isIdentity() Basic Matrix Operations

PySide2.QtGui.QMatrix.rotate(a)
Parameters:

a – float

Return type:

PySide2.QtGui.QMatrix

Rotates the coordinate system the given degrees counterclockwise.

Note that if you apply a QMatrix to a point defined in widget coordinates, the direction of the rotation will be clockwise because the y-axis points downwards.

Returns a reference to the matrix.

See also

setMatrix()

PySide2.QtGui.QMatrix.scale(sx, sy)
Parameters:

  • sx – float

  • sy – float

Return type:

PySide2.QtGui.QMatrix

Scales the coordinate system by sx horizontally and sy vertically, and returns a reference to the matrix.

See also

setMatrix()

PySide2.QtGui.QMatrix.setMatrix(m11, m12, m21, m22, dx, dy)
Parameters:

  • m11 – float

  • m12 – float

  • m21 – float

  • m22 – float

  • dx – float

  • dy – float

Sets the matrix elements to the specified values, m11 , m12 , m21 , m22 , dx and dy .

Note that this function replaces the previous values. QMatrix provide the translate() , rotate() , scale() and shear() convenience functions to manipulate the various matrix elements based on the currently defined coordinate system.

See also

QMatrix()

PySide2.QtGui.QMatrix.shear(sh, sv)
Parameters:

  • sh – float

  • sv – float

Return type:

PySide2.QtGui.QMatrix

Shears the coordinate system by sh horizontally and sv vertically, and returns a reference to the matrix.

See also

setMatrix()

PySide2.QtGui.QMatrix.translate(dx, dy)
Parameters:

  • dx – float

  • dy – float

Return type:

PySide2.QtGui.QMatrix

Moves the coordinate system dx along the x axis and dy along the y axis, and returns a reference to the matrix.

See also

setMatrix()